Introduction
In this blog, we will learn about each of the bitwise operators along with their uses in each situation. Why use bitwise operators when we have other operators to use? That's because they allow greater precision and require fewer resources and can make code faster and more efficient. They operate on each bit of a number written in binary. Let's check out some of the bitwise operators used:
&- Bitwise and|- Bitwise or<<- Left shift>>- Right shift^- xor~- negation
The truth table is a mathematical table that shows all possible outcomes that would occur from all possible scenarios that are considered. So, the truth table for the above bitwise operators is:
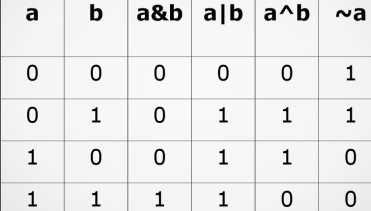
Learning the truth table is very essential, but do you need to memorize this? Check out below what each operator does so that there is no need for memorizing.
Bitwise & and |
Bitwise AND &: Zeroes win.
The bitwise AND operator ( & ) compares each bit of the first operand to the corresponding bit of the second operand. If both bits are 1, the corresponding result bit is set to 1. Otherwise, the corresponding result bit is set to 0. Both operands to the bitwise AND operator must have integral types.

Bitwise OR - | : Ones win
A bitwise OR is a binary operation that takes two bit patterns of equal length and performs the logical inclusive OR operation on each pair of corresponding bits. The result in each position is 0 if both bits are 0, while otherwise, the result is 1.

You might have seen this & and this &&, or this | and ||. This is the part where some of the folks might get confused. Where do we use Bitwise OR (|) and where do we use logical OR (||)?

The bitwise or | is used to carry out bitwise operations. Whereas logical or can be used to evaluate a condition. Let's see the cases in which both of them are used.
Consider the expression : 7 | 5. What is its value?
0000 0111 7
0000 0101 5
_____________
0000 0111 7
The answer is 7 after performing bitwise OR.
let us consider the expression 7 || 5. What is its value?
We don't operate bitwise, but the number as a whole. Any number other than 0 is considered 1. So the expression 7 || 5 equals 1 || 1 . We know 1 || 1 is 1. So the final answer is 1.

Determining odd or even using Bitwise AND
Let us consider a number n. First, let us assume it is even, then it must be divisible by 2. Since all the other bits are powers of 2, the value of their sum will result in an even number except for the 0ᵗʰ bit. This means that the 0ᵗʰ bit should be zero for sure if the number is even. So, the 0ᵗʰ bit determines whether the number is odd or even.
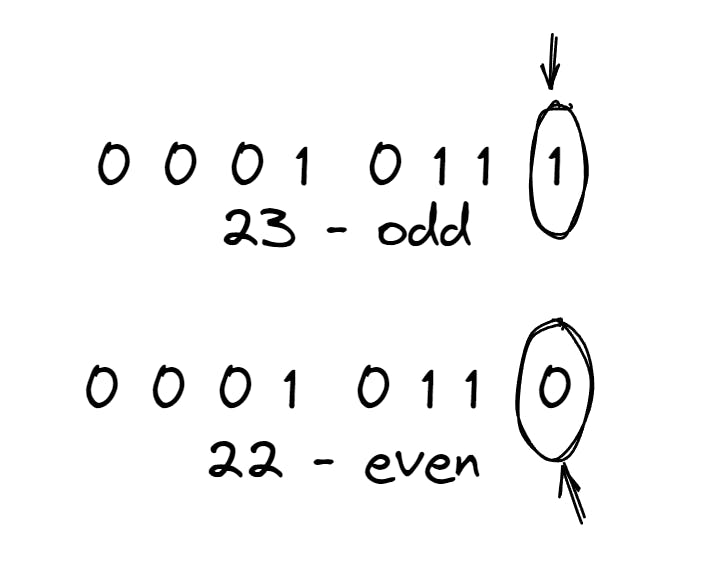
So, how do we grab the 0ᵗʰ bit?
You can use & operator to do that. When you do n & 1, then you get the value of the last digit. What you are essentially doing is :
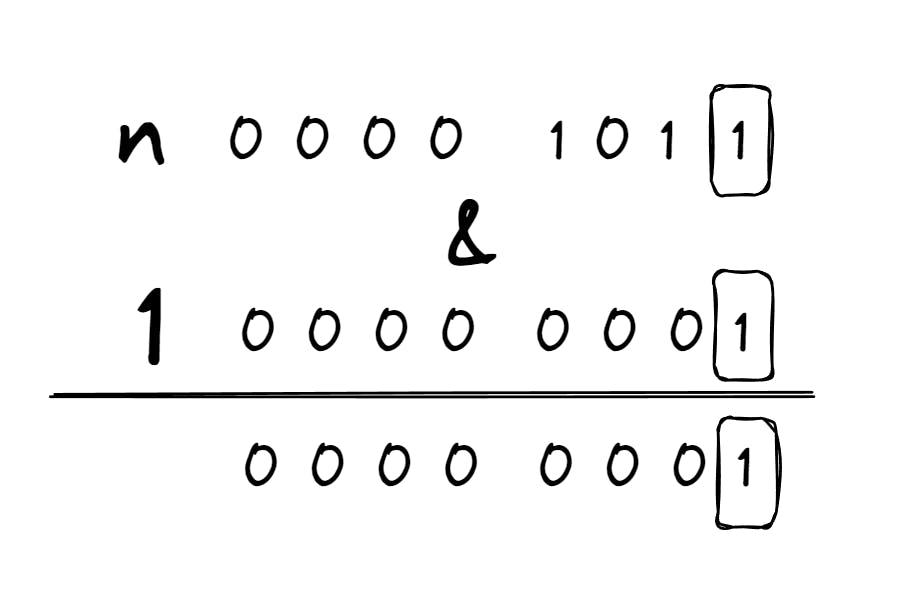
Consider the binary representation of n is 0000 1011. When you perform n & 1, 0000 1011 & 0000 0001. So this gives 0 if the 0ᵗʰ bit is 0 and 1 if it is 1. In this case, it is one so, 0000 1011 & 0000 0001 evaluates to 1, implying the number is odd.
Left shift operator <<
The left shift operator shifts all the bits in the binary representation of the number by n bits to the left side and adds the corresponding '0' bits at the end.

Everybody take a step to the left!
Let's try an example: 5 << 1
The 8-bit binary representation of 5 is 00000101. So we need to perform 00000101 << 1. So on shifting the bits to the left, 0000 1010.
What if it is 5 << 2?
Then you need to shift two bits to the left. The 8-bit binary representation of 5 is 0000 0101. Shift two bits to the left. So, after shifting once it is 0000 1010 and shifting for the second time, it is 0001 0100.
Unleashing the power of the left shift
If you followed the above two examples,5 << 1 is 0000 1010. Try evaluating it. The decimal value of it is 10. Similarly, evaluate 5 << 2 . The decimal value of 0001 0100 is 20. Do you see any pattern?
The value gets doubled in the first case and it becomes 4 times in the second case. So, we can generalize that the value is getting multiplied by 2ⁿ where n is the number of bits it is getting shifted.
So, n << k equals n X 2ᵏ.

Why is the value getting multiplied by powers of 2?
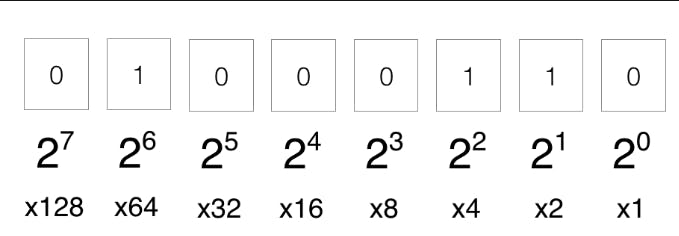
This is the way a number is represented in binary. When you shift the bits to the left once, then each bit is multiplied by 2ᵏ⁺¹ when initially, they were being multiplied by 2ᵏ. Since each of the bit values is doubled while adding to convert from binary to decimal so, the total value is also doubled.
Right shift operator >>
The right shift operator shifts all the bits in the binary representation of the number by n bits to the right side and adds the corresponding '0' bits at the start.

Everybody take a step to the right!
Let's try an example: 5 >> 1
The 8-bit binary representation of 5 is 00000101. So we need to perform 00000101 >> 1. So on shifting the bits to the right, 0000 0010.
What if it is 5 >> 2?
Then you need to shift two bits to the right. The 8-bit binary representation of 5 is 0000 0101. Shift two bits to the right. So, after shifting once it is 0000 0010 and shifting for the second time, it is 0000 0000.
so n >> k equals integer division of n / 2ᵏ.
Unleashing the power of the right shift
If you followed the above two examples,
5 >> 1 is 0000 0010. Try evaluating it. The decimal value of it is 2. Similarly, evaluate 5 >> 2 . The decimal value of 0000 0000 is 0. What do you observe from these two examples?
The value gets divided by 2 (integer division) each time the bits are shifted to the right.
Why does the value get halved?
The explanation is similar to that of the left shift. Always try tracing it out on paper for better understanding. While each bit gets shifted to the right, the value contributed by that bit also halves. Hence the total number is divided by 2.

In case you are confused about the direction in which the bits move, the bits move in the direction their symbol points to.
Some properties of bitwise operators
They obey the commutative property that a & b is the same as b & a.
They follow the Associative property that a & (b & c) is the same as (a & b) & c.
Negation ~

Everybody, flip yourself!
Every bit flips itself, if it is 1, it becomes 0 and if it is 0, it becomes 1. Let's learn about it with an example.
Ex: Let's take ~5: The binary representation of 5 is 0000 0101. So, ~5 should be 1111 1010.
XOR ^

The same is zero, different is one
When you do XOR of two numbers, if the bits are the same then it is 0 and if the bits are different then it is 1. Let's understand with the help of an example:
Let's say 5 ^ 7, then the binary representation of 5 is 0000 0101 and 7 is 0000 0111. On doing xor you get 0000 0010 which is 2. Remember same is zero and different is one.
Some common questions
Let's try solving some questions, which would help you build up the logic in other bitwise-related questions.
Checking if iᵗʰ bit is set or not
A bit is said to be set if the bit is 1. Now we need to check if the iᵗʰ bit in the binary representation of a number is set or not. If you checked the odd and even using & operator above, then we essentially checked if the 0ᵗʰ bit is set or not. Now we need to check if the iᵗʰ bit is set or not.
We can tackle this through two methods:
Keep on using the right shift operator for i times and then check if the 0ᵗʰ bit is set or not.
Take 1 and use the left shift to position 1 under the iᵗʰ bit and then find the set bit by using & operator (similar to checking if the 0ᵗʰ bit is set or not)
Let's explore the first method. Let's simulate the step-by-step process of right-shifting a number and checking the iᵗʰ bit using the example num = 23 and i = 2.
The binary representation of 23 is 0001 0111. iᵗʰ bit is 2. So, the 2ⁿᵈ bit is 1. The below picture represents the overall idea.
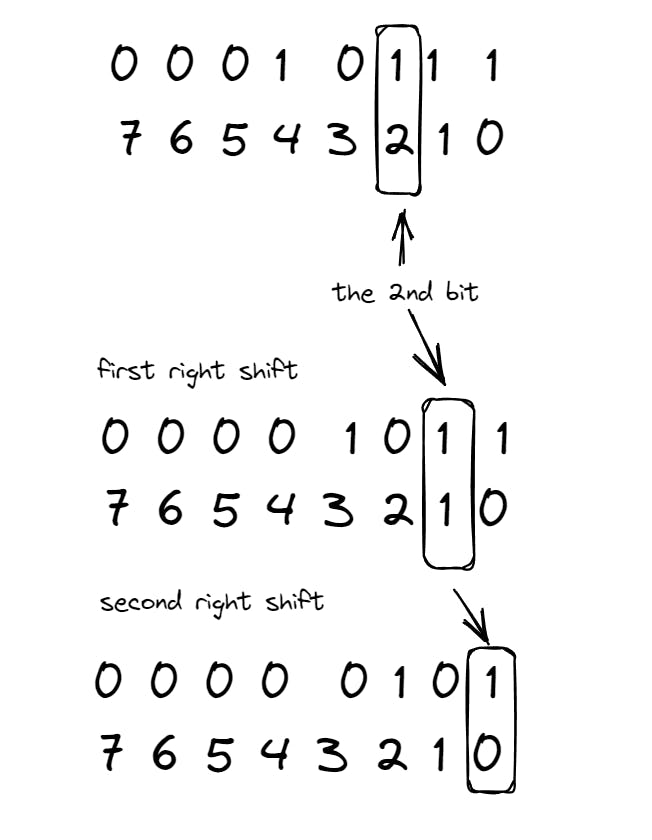
So, after right shifting 23 by 2 bits, if you were to check if the 0ᵗʰ bit is set or not, it is the same as checking if the 2nd bit is set or not.
bool checkBit(int n,int i){
return (n >> i) & 1;
}
Let's explore the second method i.e. using the left shift to shift 1s to the left and then using & operator to know whether the bit is set or not.
bool checkBit(int n,int i){
return n & (1 << i);
}
You can try the question here: https://bit.ly/3C0kAJR
Count the number of set bits
You can use either of the methods described above but with a loop. I will write it using checkBit function, you can write it without that function too.
bool checkBit(int n,int i){
return (n >> i) & 1;
}
int countSetBits(int n){
int count = 0;
for(int i = 0; i < 31; i++){
//since integer has 31 bits
if(checkBit(n,i)){
count += 1;
}
}
return count;
}
Check the Power of Two
If the number of set bits in the binary representation is 1, then it is a power of 2.
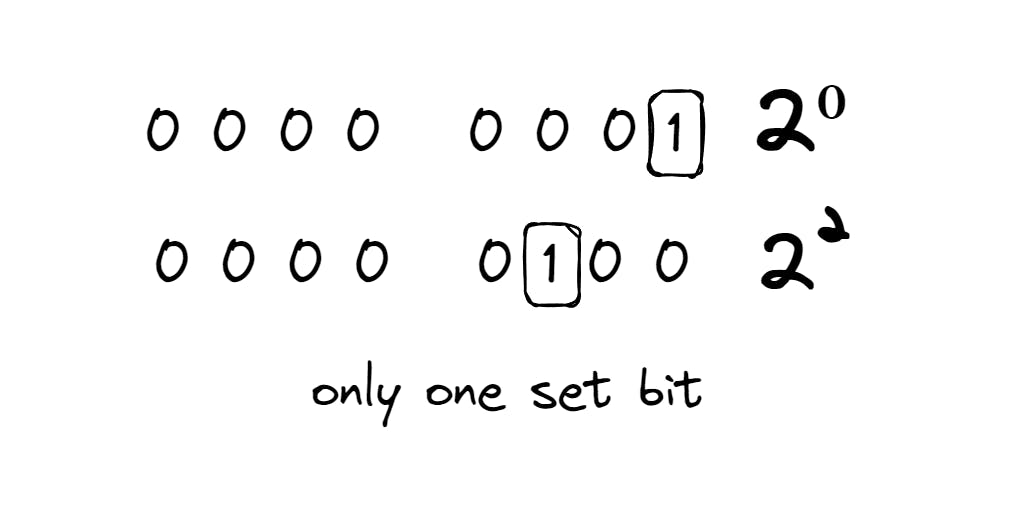
for _ in range(int(input())):
n = int(input())
c = 0
while (n) > 0:
if (n) & 1 == 1:
c += 1
n = n >> 1
if c == 1:
print("True")
else:
print("False")
You can try the question here: https://bit.ly/3R1ZPlq
Generate X 1s and Y 0s.
Break it down into two parts, let's generate X 1s first. You can do this:
Consider ans = 0. Then do the following operations for x times:
ans = ans << 1 ans = ans | 1
So you get X 1s now : 1111...x times
Now you need to generate y zeroes i.e. you just need to left shift ans by y times.
int generate(int x, int y){
int ans = 0;
for(int i = 1; i <= x; i ++){
ans = ans << 1;
ans = ans | 1;
}
ans = ans << y;
return ans;
}
Finding the unique number in a given array
If all the array elements repeat twice except one of the elements, we need to find that one element. In this case, we can use bitwise XOR. Why XOR? Remember same is 0 and different is 1. Which means n ^ n = 0.
Let's consider an array :
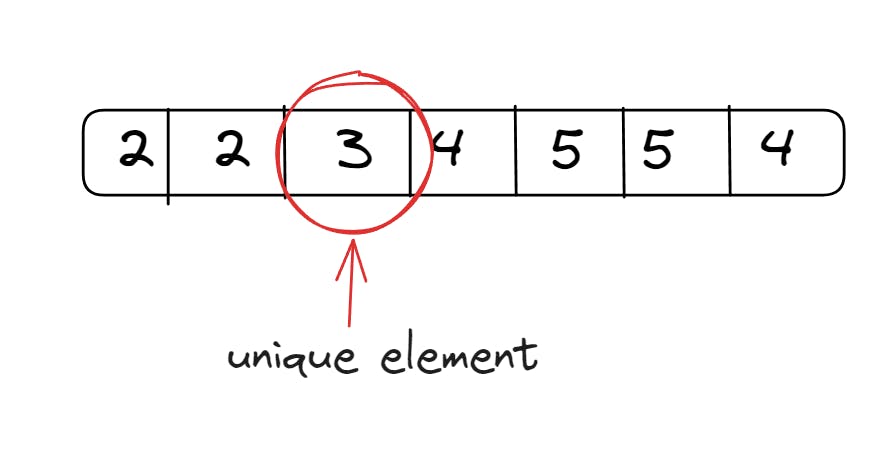
In the above array, 3 is the unique element. If you were to iterate through the array while performing an XOR operation, what would happen?
So, you would get 2 ^ 2 ^ 3 ^ 4 ^ 5 ^ 5 ^ 4 . If you referred to the properties above, then you know the associative property of bitwise operators. So, if we change their order, we can write it as 2 ^ 2 ^ 4 ^ 4 ^ 5 ^ 5 ^ 3.
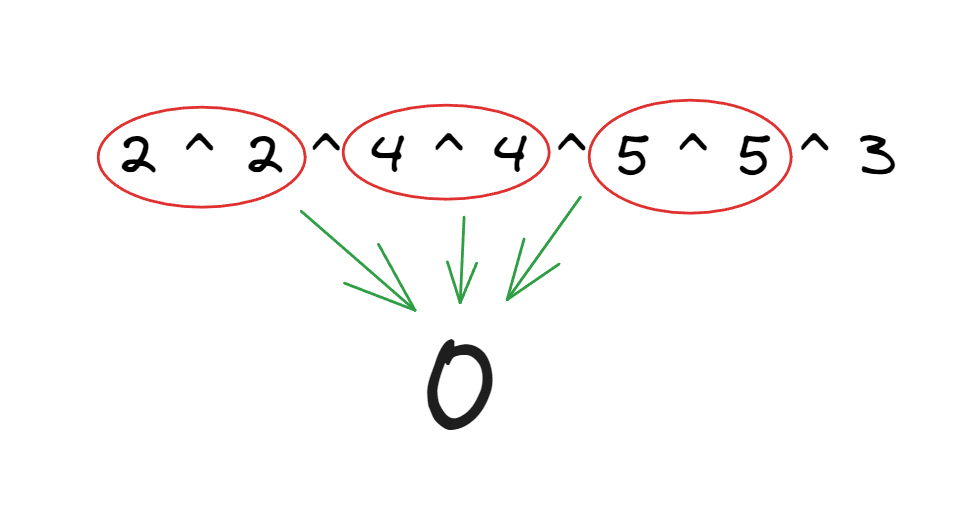
So, we need to perform 0 ^ 3 which is 3. Checkout the code below:
int arr[7] = [2,2,3,4,5,5,4];
int ans = 0;
for(int i = 0; i < 7; i++){
ans = ans ^ arr[i];
}
cout << ans << endl;
What if every element repeats thrice except one unique element? Try solving the question. It is similar to the above question.
Conclusion
You now know how the bitwise operators work and how to use each of the bitwise operators when you come across a question on it. These are the basics, try solving questions to get familiar with using them.
Let's Connect
Twitter: Shalini Muskula (@noname469717) / Twitter
Github: Shalini469717 (Shalini) (github.com)
LinkedIn : Shalini Muskula | LinkedIn
References
Images from: Bitwise Operators in GIFs (wokwi.com)
