Introduction
If you have used C/C++/Java you might have come across arrays - the boring definition of "collection of homogeneous elements". But if you have been using Python, you might have come across a list but not arrays. Lists can consist of elements of different datatypes but not arrays. So, what's the point of learning about arrays in Python when we can just use the lists? Before that let's know a bit about NumPy and get back to it.
What is NumPy?
Let's see what it is in their docs. Here's the link: NumPy Documentation.

In short, NumPy is another package in Python that can perform various mathematical operations on arrays in an easier way.
Arrays vs Lists

NumPy's arrays are more compact than Python's lists. A list of lists in Python, if it takes 20MB meanwhile NumPy's 3D arrays with single precision floats in cells would fit in 4MB.
Access to reading and writing is also faster in NumPy.
NumPy arrays have a fixed size at the time of creation, unlike lists that can grow and shrink. If you change the size of the array, then a new array is created with the elements, and the original array is deleted.
You can have heterogeneous elements in NumPy's arrays as well but it won't support the mathematical operations which defeats the purpose of using NumPy in the first place.
Installing and Importing
If you already have Python, you can install NumPy with:
conda install numpy
or
pip install numpy
To access NumPy and its functions import it in your Python code like this:
import numpy as np
We shorten the imported name to np for better readability of code using NumPy. This is a widely adopted convention that makes your code more readable for everyone working on it. Always use import numpy as np.
Arrays
Let's have a look at arrays in NumPy. An array is like a grid; you can put values in that grid and locate them with the help of their index. But the data type of all the array elements is the same.
The carton of eggs you see below is also an array. It is a 2 X 3 matrix or you can interpret it as an array of [[🥚🥚🥚][🥚🥚🥚]]. It is a 2D array. Let's learn more about them.

There are 1D arrays which consist of only a single row, and 2D arrays which consist of rows and columns. And yes, there is a 3D array as well as an N-dimensional array where N can be any dimensional. Let's take a look at the 3D array. In case you are finding it difficult to visualize, here's a look at a 3D array as a picture and as an array.

Yeah, it is a Rubix cube with numbers and it is called a sudokube. You can represent it as
arr = [[[9,7,1],[2,4,8],[5,3,6]],[[3,9,7],[6,1,5],[8,2,4]]]
If you find the above notation hard to understand, look at it this way, the 3D cube consists of 6 faces. But I don't essentially need to have all 6 faces. Write the configuration of one of the faces as you write for a 2D array. Now put it inside another array - that's it you have a 3D array now.
Let's convert our lists to arrays.
#Wait! Don't just jump into the code, import numpy
import numpy as np
#1D arrays
my_list = [1,2,3,4]
my_arr = np.array(my_list)
print(arr)
#2D arrays
matrix = [[1,2,3],[2,3,4]]
my_mat = np.array(matrix)
print(my_mat)
In case you are wondering I am using snake_case instead of CamelCase, it is a standard convention in Python.
Now, let's try some more methods which will show you how to create an array with a sequence of elements. It's a continuation of the above code, so I am not importing NumPy in the below ones.
# if you want an array with elements in a range - use arange
# it is np.arange(low,high,step) and high is not considered just like in range
arr = np.arange(0,10) # arr = [0,1,2,3,4,5,6,7,8,9]
arr = np.arange(0,10,2) # arr = [0,2,4,6,8]
If you want zeroes as all the elements in your array:
# 1D array with all elements as zeroes.Note that they are floating point.
arr = np.zeros(3) # arr = [0., 0., 0.]
# 2D array with all elements as zeroes
arr = np.zeros((2,3))
# arr = [[0., 0., 0.],[0., 0., 0.]]
If you're going to have ones as all the elements in your array:
# 1D array with all elements as ones.Note that they are floating point.
arr = np.ones(3) # arr = [1., 1., 1.]
# 2D array with all elements as ones
arr = np.ones((5,6))
# arr = [[1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1., 1.]]
#It is similar to the zeroes case.
If you don't want the floating point, you can specify the data type you want
x = np.ones(2, dtype=np.int64) #x = array([1, 1])
If you're going to divide a range into some points and then get the points, you can use linspace .
#gives evenly spaced points where 3rd argument is the number of points
arr = np.linspace(0,10,10)
# arr = [ 0. , 1.11111111, 2.22222222, 3.33333333, 4.44444444,
# 5.55555556, 6.66666667, 7.77777778, 8.88888889, 10. ]
Identity Matrix
#identity must be square so we need to pass only one number as argument
arr = np.eye(5)
# arr = [[1., 0., 0., 0., 0.],
# [0., 1., 0., 0., 0.],
# [0., 0., 1., 0., 0.],
# [0., 0., 0., 1., 0.],
# [0., 0., 0., 0., 1.]]
Random Numbers
Let's fill the array with random numbers!
#random integers in certain range
#It will differ for you as it is generated randomly
arr = np.random.randint(10,20,6) #[14,16,18,19,15,17]
#you can fill the array with numbers from uniform distribution too!
#Used to describe probability where every event has equal chances of occuring
arr = np.random.rand(2) #[0.67408218, 0.6168245 ]
#normal distribution - yup you missed your math class
np.random.randn(5) #[ 0.9077414, -1.4007080, 0.0035573, -1.0919055, 0.7274706]
Reshaping
The number of dimensions and items in an array is defined by its shape. The shape of an array is a tuple of non-negative integers that specify the sizes of each dimension. For example, for a 2 x 3 matrix or an array having 2 rows and 3 columns, then you can represent the shape of the array by a tuple as (2,3).
If you want to reshape your array, note the number of elements should be the same before and after reshaping. Let's say you have a 1 x 10 array such as [1,2,3,4,5,6,7,8,9,10]. Now you can reshape it to a 2 X 5 array which is a 2D array. But the elements initially were 1x10 = 10 elements and finally also, 2x5 = 10 we have 10 elements.
arr = np.random.randint(10,20,6) #[17 11 17 15 14 10]
arr.shape #notice there is no (). The output is (6,)
arr.reshape(2,3)
# arr = [[17, 11, 17],
# [15, 14, 10]]
Contcatanation and Sorting
Let's talk about axes in NumPy. Axes are defined for arrays with more than one dimension. A 2-dimensional array has two corresponding axes: the first running vertically downwards across rows (axis 0), and the second running horizontally across columns (axis 1).
# It is similar to sorting using lists
arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])
np.sort(arr)
#concatanating arrays
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
arr = np.concatanate((a,b)) # arr = [1,2,3,4,5,6,7,8]
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6]])
arr = np.concatenate((x, y), axis=0)
# arr = [[1, 2],
# [3, 4],
# [5, 6]]
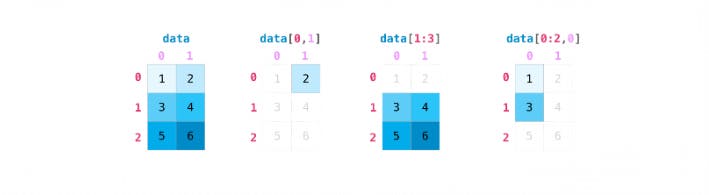
Indexing and slicing
You can see visually how indexing and slicing work. This is similar to that of indexing and slicing in lists.
data = np.array([1, 2, 3])
data[1] #accessing element at index 1
#array of elements from index 0 to index 2 excluding element at index 2
data[0:2] #array([1, 2])
#array of elements starting from 1 and goes till the end
data[1:] #array([2, 3])

Now, let's see indexing and slicing in 2D arrays.

data = np.array([[1, 2], [3, 4], [5, 6]])
# to select element present in 0th row and 1st column
data[0, 1] #1
#select elements present in rows 1-2
data[1:3] #array([[3, 4],[5, 6]])
#select elements present in rows 0-1 and column 0
data[0:2, 0] #array([1, 3])
Array Operations
Let's say you have created an array and another array ones, NumPy allows you to add them.
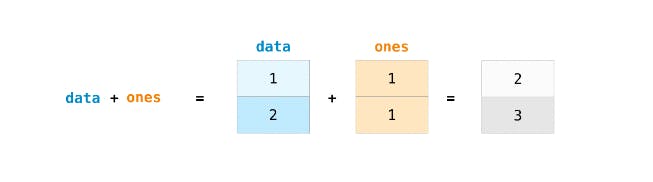
data = np.array([1, 2])
ones = np.ones(2, dtype=int)
data + ones #array([2, 3])
Similarly, you can do subtraction, multiplication, and division too!
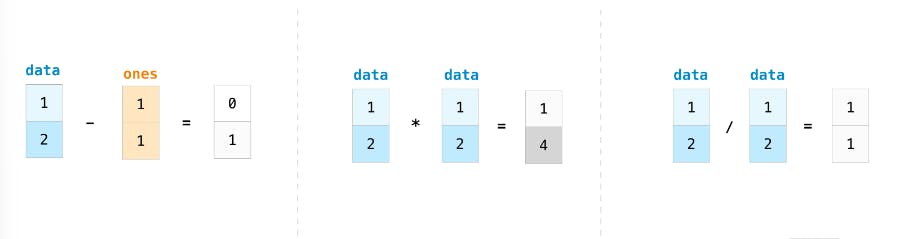
data - ones #array([0, 1])
data * data #array([1, 4])
data / data #array([1., 1.])
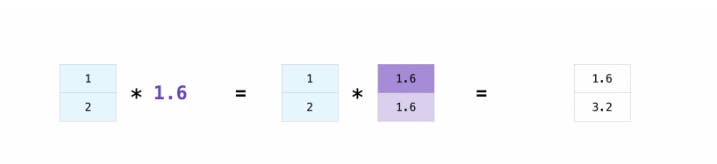
data = np.array([1.0, 2.0])
data * 1.6 #array([1.6, 3.2])
Not only arrays, but you can also perform operations with numbers.
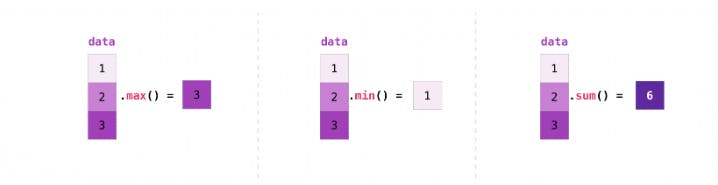
You can get maximum and minimum elements of the array too!
data = np.array([1.0, 2.0,3.0])
data.max() #3.0
data.min() #1.0
data.sum() #6.0
Docs
This isn't all there is to NumPy, it is vast and the documentation is your sole guide. It contains all the necessary elements required for you to get started and answer all your questions.

Let's Connect
Twitter: Shalini Muskula
Github: Shalini469717 (Shalini) (github.com)
LinkedIn : Shalini Muskula | LinkedIn
